The famous QR factorization algorithm can be BLAS-3 optimized. Using the Woodbury matrix identity, we implement a block-based Rank-Revealing QR and point out a connection between pivot selection and object detection.
QR Decomposition
A square matrix 
has a factorization
![\[A = QR\]](https://www.alexwei.net/wp-content/ql-cache/quicklatex.com-7cec3f34ed3d0429ab6dd937a9670e82_l3.png "Rendered by QuickLaTeX.com")
with orthogonal matrix 
and upper triangular 
. A is transformed into R by a successive series of Householder reflectors
![\[H_i \doteq I - 2 v v^T\,,\quad v = \begin{bmatrix} \|a_i\| \\ 0 \\ \vdots \end{bmatrix} - a_i\]](https://www.alexwei.net/wp-content/ql-cache/quicklatex.com-398f8b3b84384fe1be063b75be14cfb2_l3.png "Rendered by QuickLaTeX.com")
of columns 
in 
. The i’th step of the factorization algorithm operates on the i’th column of 
. After 
steps, the first columns of the resulting 
are triangularized.
Triangularization can be done in any column order by swapping columns between each step and agglomerating the swaps into a permutation/pivot matrix 
![\[Q^{-1} A P = \prod H_i A P = R \iff QRP^{-1} = A \,.\]](https://www.alexwei.net/wp-content/ql-cache/quicklatex.com-c654277a8b1ff7ba19f686be98b4b8cc_l3.png "Rendered by QuickLaTeX.com")
When done in order of greatest column rank, this is called the strong Rank Revealing QR factorization (RRQR). In addition to being more numerically stable, the RRQR provides spectral information of the matrix by virtue of the pivot selection without additional computation of column norms. Columns may instead be sampled if spatially relevant, or convolved and filtered as the basis of an indicator-transform in the case of object detection.
Pivot Selection for Image Input
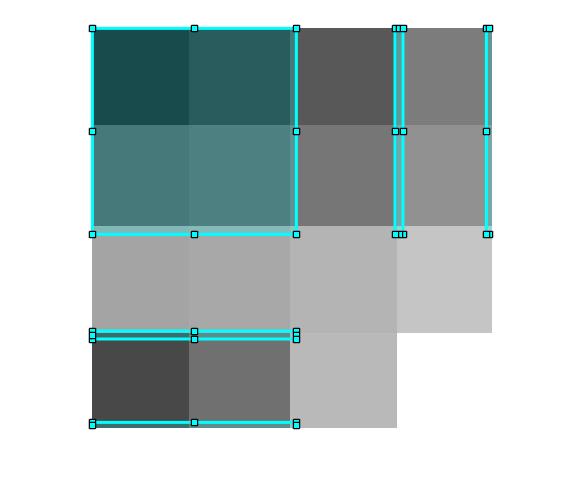
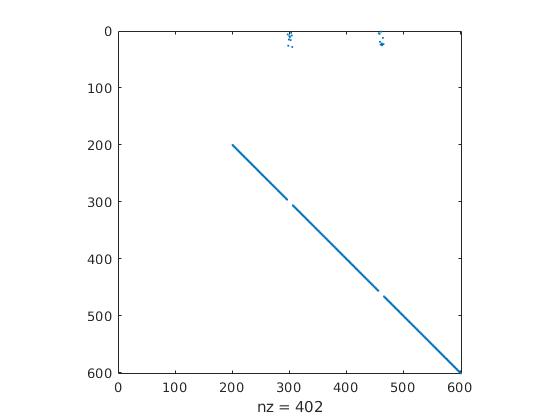
corresponding to a one-sided triangularization of grayscale image (r)If the matrix encodes a grayscale image such as the one above, then the resulting pivot selection indicates a preference for darkest overall columns and triangularizes them first. RRQR of a grayscale image selects pivots corresponding to detected object locations inside the image and generates a spanning box grid which we compare to the objects in the original image. Applying the one-sided RRQR to an image matrix, and again another RRQR to its transpose, objects are detected by filtering the resulting pivots in 
.
RRQR Object Detection with downsampling
dim col A’ = .3 * dim col A
dim col A’ = .2 * dim col A
On a uniform grid of objects, object detection by RRQR remains consistent even for a downsampled matrix
![\[A' = (A^T G)^T\,,\quad \text{Gaussian matrix }G\,.\]](https://www.alexwei.net/wp-content/ql-cache/quicklatex.com-2a62924f0b4fff9cb891adcd4e13e77d_l3.png "Rendered by QuickLaTeX.com")
Check out the PDF below for MATLAB code and further discussion,
